1.图像编码原因:
传递数据信息时,通常相同的信息量可以通过不同大小的数据量去表示,显然小数据量去表示大信息量是效益最高的,而图像编码即是尝试用不同的表达方式以减少表示图像的数据量,对图像的压缩可以通过对图像的编码实现。
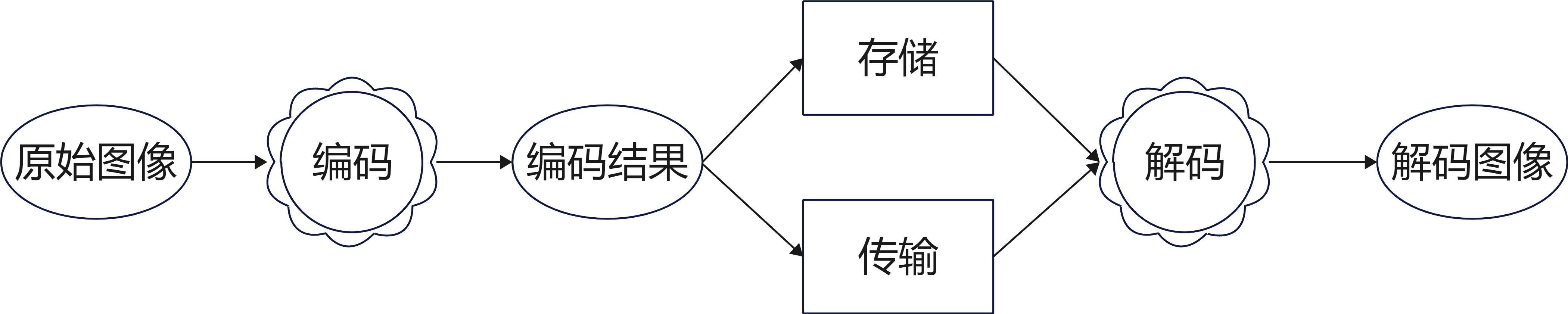
2.数据压缩
减少表示给定信息所需要的数据量,包含不想管和重复信息的数据惩治为冗余数据。数据压缩的目的就是消除冗余数据。
2.1 压缩率和相对冗余度
压缩率: \(C=\frac{n_{1} }{n_{2} }\), 相对冗余度:\(R=\frac{n_{1}-n_{2}}{n_{1}}=1-\frac{1}{C}\)
其中,\(n_{1}\)为压缩前的数据量(比特数),\(n_{2}\)为压缩后的数据量。
2.2 静态图像冗余类型
2.2.1 编码冗余
编码是用于表示信息实体和时间集合的符号系统(字母、数字。比特和类似的符号等)。
- 码字: 每个信息和事件(灰度值)被赋予了一个编码符号的序列(0x00-0xFF)
- 码长: 码字中的符号数量(8)
- 码本: 构成码字的所有编码符号的集合(0和1)
每个像素的平均比特数
\[L_{avg}=\sum_{k=0}^{L-1}l(r_{k})p_{r}(r_{k})\]
其中\(r_{k}\)为某一灰度值, \(p_{r}(r_{k})\)为该灰度值使用的码字的码长(即所用的比特数),根据上式可以得出\(L_{avg}\)
注:
- 1.如果用较少的比特数表示出现概率较大的灰度级,用较多的的比特数表示概率较小的灰度级,得到的平均比特数较小。
- 2.如果平均比特数不能达到最小,就说明存在编码冗余。
- 3.冗余度越大,可压缩量越大
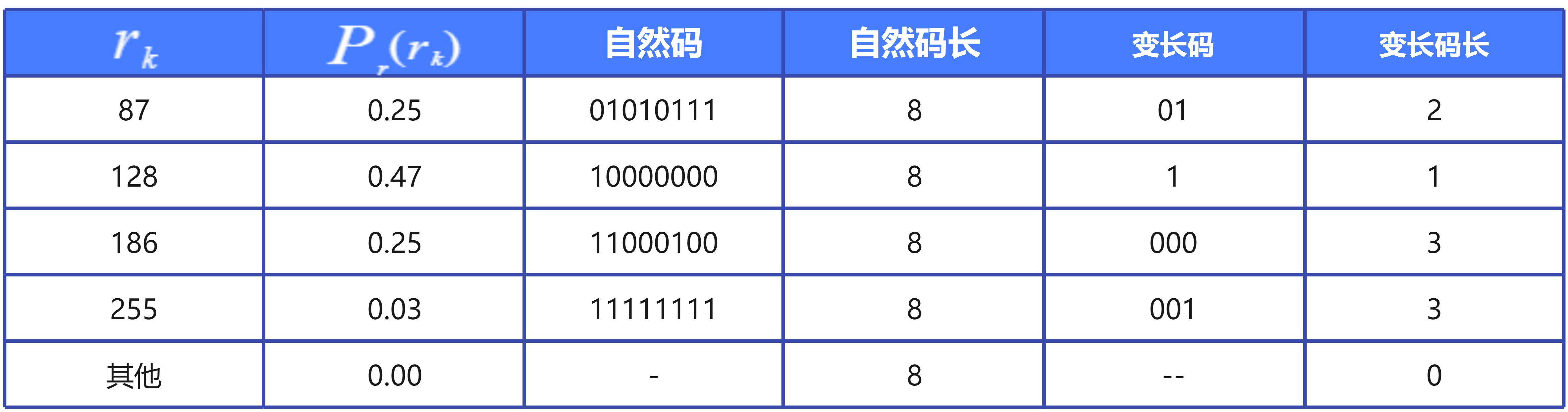
- 自然码平均码长: 8
- 变长码平均码长: 1.81
- 压缩率: 8/1.81 = 4.42
- 冗余度: 1-1/4.42 = 0.774
如上表所示,图像的像素值为0-255,可用8位自然码表示,统计图像像素值出现概率,出现概率较大的像素值用较少位数的变长码表示。
见上表,像素值128出现概率最高,,为0.47,则其所对应变长码为1。接下来出现概率第二高的变长码概率设置为10, 随后11、100、101...以此类推。
2.2.2 视觉(空间)冗余
在同一个图像中,相邻的两个像素点,会有很多色彩是很接近的,那么如很能在最后得到的图片中,尽量少得记录这些不需要的数据点,也即达到了压缩的效果。
这便涉及到了图像信号的频谱特性
图像信号的频谱线一般在0-6MHz范围内,而且一幅图像内,包含了各种频率的分量。但包含的大多数为低频频谱线,只在占图像区域比列很低的图像边缘的信号才含有高频的谱线。
因此具体的方法就是根据频谱因随分配比特数——对包含信息量大的低频谱区域分配较多的比特数,对包含信息量低的高频谱区域分配较少的比特数,而图像质量并没有可察觉的损失,以达到数据压缩的目的。
将原始图像的空间域转化为频谱域用到了数学上的离散余弦变换,即DCT(Discrete Cosine Transform)变换,DCT是基于傅里叶变换的一个变种。
2.2.3 心理视觉冗余
由于眼睛对所有视觉信息感受的灵敏度不同,以及人眼在正常的视觉处理过程中信息的相对重要程度不同,图像中的部分被视觉系统忽略的信息可以被当作是冗余信息去除。
3.信息论相关
3.1图像信息的度量
信息论中,一个具有概率P(E)的随机时间E所包含的信息量I(E)为:
\(I(E)=log\frac{1}{P(E)}=-logP(E)\)
对数的底决定了信息单位,一般取2
3.2 信号源
一幅图像可以看作一个具有随机离散输出的信源,信源可以从一个有限的符号集中产生一个随机的符号序列。
信源集 \(B=\){\(b_{1},b_{2},...,b_{j}\)}
概率矢量 \(u=\)[\(P\)(\(b_{1}\)),\(P\)(\(b_{2}\)),...,\(P\)(\(b_{j}\))]\(^T\)
3.3 熵
3.3.1 香农熵(Shannon Entropy)
香农熵是用来描述信息量的多少、随机变量不确定性的度量
- 给定一个随机变量X,有:
\[p(x)=P_{r}\{X=x\},x\in\omega\]
- 香农熵为:
\[H(X)=-\sum_{x\in\omega}p(x)log_{2}p(x)\]
3.3.2 联合熵(Joint Entropy)
衡量一对随机变量所包含的信息量,两个随机变量联合不确定性的度量,联合熵描述了随机变量的相关性,越小越相关(X,Y)及联合分布p(x,y)
\[H(X,Y)=-\sum_{x\in X}\sum_{y\in Y}p(x,y)log_{2}p{x,y}\]
3.3.3 条件熵 (Conditional Entrophy)
已知\(Y\)随机变量的前提下,随机变量\(X\)提供的信息量,根据:
\[p(x|y)=\frac{p(x,y)}{p(y)}\]
可以得到:
\[ \begin{aligned} H(X|Y)&=-\sum_{x\in X}\sum_{y\in Y}p(x,y)log_{2}p(x|y) \\ & =-\sum_{x\in X}\sum_{y\in Y}p(x,y)log_{2}p[\frac{(x,y)}{p(y)}] \\ &=H(X,Y)-H(Y) \end{aligned}\]
对于联合分布和边缘分布,把X或Y的熵称作边缘熵,于是有:
\[H(Y|X)=H(X,Y)-H(X)\]
3.3.4 累计剩余熵(Cumulative Residual Entropy, CRE)
将香农熵定义中概率分布换成累计概率分布
\[\epsilon(X)=-\sum_{x\in X}P(X>x)logP(X>x)\]
3.3.5 瑞利熵(RE)
瑞利熵是香农熵的一种推广形式,又称作\(\alpha\)熵
\[R_{\alpha}(X)=\frac{1}{1-\alpha}log\sum_{x\in X}p(x)^{a} \quad (\alpha>0,\alpha \neq 1)\]
当\(\alpha\rightarrow1\),求得瑞利熵的极限为香农熵,求极限用洛必达法则即可
3.4 相似性度量
3.4.1 互信息(Mutual Information, MI)
互信息衡量随机变量\(X\),\(Y\)之间的依赖程度,用来测量联合概率分布和二者完全独立时的分布之间的距离,使用KL散度(或称为相对熵)来定义
\[MI(X,Y)=\sum_{x}\sum_{y}p(x,y)=log\frac{p(x,y)}{p(x)\cdotp(y)}\]
互信息、联合熵、边缘熵、条件熵之间有紧密的关系
\[\begin{aligned}MI(x,y)&=H(X)+H(Y)-H(X,Y)\\ &=H(X)-H(X|Y)\\ &=H(Y)-H(Y|X)\end{aligned}\]
互信息表示\(X\)中包含\(Y\)的信息的多少,也就是对称的\(Y\)中包含\(X\)的多少。若\(X\),\(Y\)独立则\(I(X,Y)=0\) ,若一一相关,则\(I(X,Y)=H(X)=H(Y)\)
3.4.2 归一化互信息(Normalized Mutual Information,NMI)
为了解决互信息对图像部分重叠区域的敏感性,NMI应运而生
\[NMI(X,Y)=\frac{H(X)+H(Y)}{H(X,Y)}\]
3.4.3 熵相关系数(Entropy Correlation Coefficient, ECC)
可以看作为另一种归一化信息方法
\[\begin{aligned}ECC&=\frac{2I(X,Y)}{H(X),+H(Y)}\\ &= 2-\frac{2}{NMI}\end{aligned}\]
3.4.4 互累计剩余熵(Cross Cumulative Residual Entropy,CRE)
和互信息类似,只不过这里的熵换成了累计剩余熵
\(CCRE(X,Y)=\epsilon(X)-E[\epsilon(Y|X)]\)
3.4.5 Alpha互信息(Alpha Mutual Information ,\(\alpha-MI\alpha-MI\))
顾名思义,根据\(\alpha\)熵得出\(\alpha\)熵
\[D_{\alpha}=\frac{1}{\alpha-1}log \sum_{x\in X} \sum_{y\in Y}p(x,y)^\alpha(p(x)p(y))^{1-\alpha}\]
3.4.6 相对熵(KL散度)
相对熵也称作为KL散度,可以衡量两个分布之间的差异,\(p,q\)是\(x\)上的两个分布
\[D_{KL}(P||q)=\sum p(x)log\frac{p(x)}{q(x)}\]
3.4.7 交叉熵
交叉熵是KL散度的一部分
\[H(p,q)=\sum_{x\in X}p(x)log(q(x))\]
3.4.8 詹森香农散度(JS散度)
因为KL散度不对称,所以詹森提出了JS散度
\[JS(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2}))\]
3.4.9 詹森瑞利散度
詹森香农散度与瑞利熵的结合
\[JR_{\alpha}^{\omega}(X,Y)=R_{\alpha}(Y)-\sum_{x\in X}p(x)R_{\alpha}(Y|x)\]
参考资料:
- [1] 图像中用到的信息论中的一些概念公式
- [2] 图像编码技术