1.JPEG概述
JPEG是Joint Photographic Experts Group的缩写,即ISO和IEC联合图像专家组,负责静态图像压缩标准的指定,这个专家组开发的算法就被称为JPEG算法,并且已经成为大家通用的标准,即JPEG标准。JPEG压缩是有损压缩,但这个损失的部分是人的视觉不容易察觉到的部分,他充分利用了人眼对计算机色彩中高频信息不敏感的特点,来大大节省了需要处理的数据信息。
1.1 去除视觉上的多余信息
由于人眼的视觉生理特性,人眼对不同频率成分有不同的敏感度
- 如人眼含有对亮度敏感的柱状细胞1.8亿个,含有对色彩敏感的椎状细胞0.08亿个。故眼睛对亮度的敏感程度要大于对色彩的敏感程度。
总体而言,一个原始图像信息,要对其进行JPEG编码,过程分两大步:
- 去除视觉上的多余信息,即空间冗余度
- 去除数据本身的多余信息,即结构(静态)冗余度

如上图,除了表示图像像素的位置水平X轴和垂直Y轴以外,还有一个表示色彩值的Z轴。Z代表了三元色各个分支R/G/B的混合时所占的具体数值大小,每个像素的RGB的混合值可能都不同,但是临近的两个点的R/G/B三个值会比较接近。
1.2 去除数据本身的多余信息
利用Huffman编码,来将最后的数据用无损的方式做压缩,这个是纯数学上的处理方式。
1.3 图像信号的频谱特性
不同的颜色对应着不同的频率,图像信号的频谱线一般在0-6MHz范围内,而且一幅图像内,包含了各种频率的分量。但是包含的大多数为低频频谱线,只在占图像区域比例很低的图像边缘信号中才含有高频谱线。——这是JPEG对图像压缩的理论依据
具体的做法即使为:在对图像做数字处理时,可根据频谱因素分配比特数:对包含信息量大的低频谱区域分配较多的比特数,对包含信息量少的高频谱区域分配较低的比特数,而图像质量并没有可察觉的损伤,以达到数据压缩的目的。
总体来说,上面的几步即是:
如果处理的是彩色图像,JPEG算法首先将RGB分量转化成亮度分量和色差分量,同时丢失一般的色彩信息(空间分辨率减半)。然后,用DCT来进行块变换编码,舍弃高频的系数,并对余下的系数进行量化以进一步减少数据量。最后,使用RLE行程编码和Huffman编码来完成压缩任务
2.JPEG原理详解
下面将更加详细地介绍这两步中的各个细节。
JPEG编码中主要涉及到的内容主要包括:
- Color Model Conversion(色彩模型)
- DCT(Discrete Cosine Transform 离散余弦变换)
- 重排列DCT结果
- 量化
- RLE编码
- 范式Huffman编码
- DC的编码

2.1 色彩空间 color space
在图像处理中,为了利用人的视角特性,从而降低数据量,通常把RGB空间表示的彩色图像变换到其他色彩空间。
现在采用的色彩空间有三种:YI1,YUV,YCrCb
每一种色彩空间都产生了一种亮度分量信号和两种色度分量信号,而每一种变换使用的参数都是为了适应某种类型的显示设备

2.2 色彩深度 color depth
一幅图像是由很多个像素点组成的,存储每个像素点所用的位数叫做像素深度。对不同的图片,这个值是可以有所不同的,从而会使得图片的数据有多和少的区别。
一幅彩色图像的每个像素用RGB三个分量表示,那么一个像素共用3*8=24位表示,就说像素的深度24bit,每个像素可以是2的24次方种颜色种的一种。表示一个像素的位数越多,它能表达的颜色数目就越多。
2.3 离散余弦变换DCT
将图像从色彩域转换到频率域,常用的变换方法有:
- 傅氏变换
- Walsh-Hadamard沃尔什哈达码变换
- 正弦变换
- 余弦变换——应用最广
- 斜变换
- 哈尔变换
- K-L变换
2.3.1 离散余弦变换预备知识
二维傅里叶可分离变换可用通用的关系式来表示
\[F(u,v)=\sum_{x=0}^{M-1}f(x,y)g(x,y,u,v)\]
\[f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)h(x,y,u,v)\]
式中:\(x,u=0,1,2,...,M-1;y,v=0,1,2,...,N-1;\)g(x,y,u,v)和h(x,y,u,v)分别称为正向变换核和反向变换核
如果满足:
\[g(x,y,u,v)=g_{1}(x,u)g_{2}(y,v)\]
\[h(x,y,u,v)=h_{1}(x,u)h_{2}(y,v)\]
则称正、反变换核是可分离的,进一步,如果\(g_{1}\)和\(g_{2}\),\(h_{1}\)和\(h_{2}\)在函数形式上一样,则称该变换核是对称的
图像变换的矩阵表示
数字图像都是实数矩阵,设\(f(x,y)\)为MxN的图像灰度矩阵,通常为了分析、推导方便,可将可分离变换写成矩阵的形式:
\[F=P\cdot f\cdot Q\]
\[f=P^{-1}FQ^{-1}\]
其中,F、f是二维矩阵\(M\times N\)的矩阵;P是\(N\cdot N\)的矩阵。
\[F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}P(x,u)f(x,y)Q(y,v)\]
式中,u=0,1,2,...,M-1,v=0,1,2,...,N-1
对于二维离散傅里叶变换,则有:
\[P(x,u)=g_{1}(x,u)=e^{\frac{-j2\pi ux}{M}}\]
\[D(y,u)=g_{2}(y,u)=e^{\frac{-j2\pi vy}{N}}\]
2.3.2 离散余弦变换数学原理
离散余弦变换(Discrete Cosine Transform,DCT)是可分离的变换,其变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。
一维离散余弦变换定义
\[g(x,u)=C(u)\sqrt{\frac{2}{N}}cos\frac{(2x+1)u\pi}{2N}\]
一维DCT定义如下:设{f(x)|x=0,1,...,N-1}为离散的信号列
\[F(u)=C(u)\sqrt{\frac{2}{N}}\sum_{x=0}^{N-1}f(x)cos\frac{(2x+1)u\pi}{2N}\]
二维离散余弦变换
二维DCT正变换核为:
\[g(x,y,u,v)=\frac{2}{\sqrt{MN}}C(u)C(v)cos\frac{(2x+1)u\pi}{2M}cos\frac{(2y+1)v\pi}{2N}\]
式子中,x,u=0,1,2,...,M-1;y,v=0,1,2,...,N-1
二维DCT定义如下:
设f(x,y)为MxN的数字图像矩阵,则:
\[F(u,v)=\frac{2}{\sqrt{MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)C(u)C(v)cos\frac{(2x+1)u\pi}{2M}cos\frac{(2y+1)v\pi}{2N}\]
式中:x,u=0,1,2,...,M-1;y,v=0,1,2,...,N-1
综上,DCT变换的公式为:
\[F(u,v)=\frac{1}{4}C(u)C(v)[\sum_{i=0}^{7}\sum_{j=0}^{7}f(i,j)cos\frac{(2i+1)u\pi}{16}cos\frac{(2j+1)v\pi}{16}]\]
f(i,j)经DCT变换之后,F(0,0)是直流系数,其他为交流系数。

上图为8x8的原始图像,将原始图像推移128,使其范围变为-128~127

使用离散余弦变换,并四舍五入取最接近的整数

经过以上操作,取样块便从时间域转化成了频率域的系数块。
DCT将原始图像信息块转换成不同频率分量的系数集,有两个优点
- 信号常将其能力大部分集中于频率域的一个小范围内,这样一来,描述不重要的分量只需要很少的比特数。
- 频率域分解映射了人类视觉系统的处理过程,并允许后继的量化过程满足其灵敏度的要求。
2.4 量化
量化过程实际上就是对DCT系数的一个优化过程。它是利用了人眼对高频部分不敏感的特性来实现数据的大幅简化。量化为整个过程中主要的有损运算。
- 量化过程实际上是简单地把频率领域上每个成分,除以一个对于该成分的常数,且接着四舍五入取最接近的整数。

因为人眼对亮度信号比对色差信号更敏感,因此使用了两种量化表:亮度量化值和色差量化值

使用量化矩阵以及前面所得到的DCT系数矩阵,可以结合DC系数四舍五入得到最接近的整数
\[取整(\frac{-415}{16})=取整(-25.9375)=-26\]
总体而言,DCT变换实际上是空间域的低通滤波器——对Y分量采用细量化,对UV分量采用粗量化
2.5 Z字编排
量化后的数据有很大一个特点,即是直流分量相对于交流分量来说要大,而且交流分量中含有大量的0。

此时边可采用"Z"字形编排的方法,通过"Z"字编排,数据在交流分量的维度上会出现很多0值连续的状况。在"Z"字形编排的基础上结合行程编码,将会很大程度上降低了编码的大小。
2.6行程编码
行程编码(Run Length Coding)又称为"运行长度编码"或"游程编码",它是一种无所压缩编码。
例如:5555557777733322221111111
这一串数据的一个特点是相同的内容会出现很多次,那么我们就可以用一种简化的方法来记录这一串数字,如:
(5,6) (7,5) (3,3) (3,4) (1,7)
2.7范式 Huffman编码
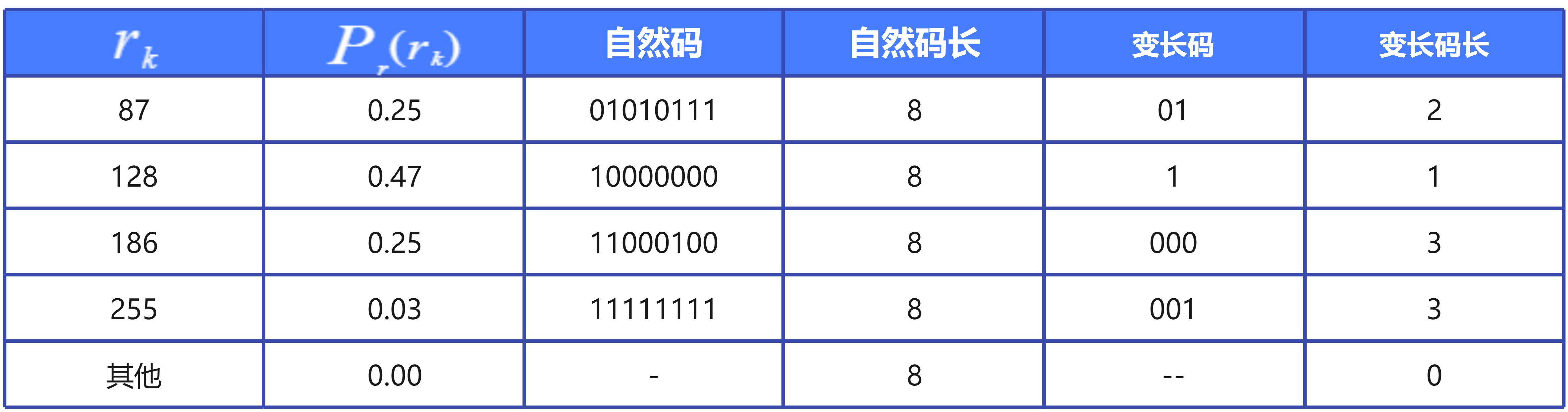
范式Huffman编码(Canonical Huffman Code)是一个按数据出现的概率进行编码的一种编码方式,很多流行的压缩方法都使用了范式哈夫曼便阿门技术,如GZIB、ZLIB、PNG、JPEG、MPEG等等。
压缩原理与下图类似:
3.JPEG文件存储格式
通常我们保存的文件名后缀为jpg,但按标准来说,它是一种JFIF格式标准的文件,里面的图像压缩方式是JPEG。
JFIF是一个文件格式标准,JPEG是一个压缩标准,不是一个概念
JFIF是File Interchange Format的缩写,也即JPRG文件交换格式。JFIF是一个图片文件格式标准,它是一种使用JPEG图像压缩技术存储摄影图像的方法。JFIF代表了一种"通用语言"文件格式,它是专门为方便用户在不同的计算机和应用程序见传输JPEG图像而色痕迹的语言
JFIF文件格式定义中的一些内容是JPEG压缩标准未定义的,如resolution/aspect ratio,color space等
参考资料:
[1] JPEG 图片压缩原理(一)
[2] 离散余弦变换原理及实现
[3] 图像编码基础